In this last example we'll get ourselves familiar with a powerful concept, which is used on many programming languages today: Recursion. It basically means that a function calls itself over and over again (but, of course, not endlessly). For this we'll consider the following:

A first simple example

The task in this example is a simple one (example3.map): Walk as far as you can (i.e. until you reach a wall), turn around go back the same distance -- which means that the robot should stop at the same field it started in the beginning. This seems to involve some kind of counting ("How many moves has the robot made?") but unfortunately our robots don't have such abilities.

So after reaching the wall, how do we know how many fields to go back? We'll have to come up with some way of 'implicit' counting. Let's take a systematic approach and analyse what we want to do: We go one field forward and check whether we face a wall. In case we do, we turn around and go back -- but we go back exactly the number of fields we crossed before! This is where recursion comes into play. I'll start by giving the final code and then explaining it:

main =
 go_forward &>
 IfThenElse front_free
  main
  turn_around &>
 go_forward

turn_around = turn_right &> turn_right

The decisive part is where main calls itself again (marked italic above). Note that at this point the function is not finished yet, there are some commands left (actually only one command, needed for going back one field) -- they are, as usual, stored inside the robot's memory until the call to the sub-function has finished. This means that for every field we cross the instructions for passing it on the way back are kept inside the robot's memory, regardless of the recursive call to main.

We are going to use the very same idea in the next example which is essentially the same.

Recursive stairs

Our robot is standing on some stairs (not necessarily at the bottom) and we know that an item is lying on one of the steps somewhere upstairs, which we want to pick up. This is not tough yet, we could easily solve that with our current knowledge. But after picking up the item we want to go back downstairs to exactly the stair we started at.

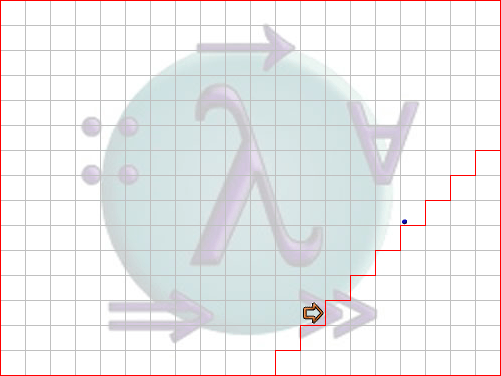
So after picking up the item, how do we know how many stairs to go down? Again we analyse what we want to achieve: We go up one stair and check whether we found the item. In case we did, we take it, turn around and go down, again exactly the number of stairs we climbed up before! Now we can use the principle of recursion as in the previous example:

main = one_stair

one_stair =
 stair_up &>
 IfThenElse field_has_item
  (take_item &> turn_around)
  (one_stair) &>
 stair_down

stair_up = turn_left &> go_forward &> turn_right &> go_forward
stair_down = go_forward &> turn_left &> go_forward &> turn_right
turn_around = turn_right &> turn_right
turn_left = turn_around &> turn_right

For this example we can draw the following 'recursion diagram', where the same level of identation means that the actions are on the same 'recursive level', i.e. they are part of the same function call:

stair_up
    stair_up
        stair_up
            stair_up
            -> Item found, take it and turn around, recursion end
            stair_down
        stair_down
    stair_down
stair_down

We observe that the stair_down of the first call is actually executed last. This is because it is put into memory first and all subsequent commands are put "on top" and are therefore executed prior to the first stair_down.

Let's build some strange stairs

Now we are going to make the task a little tougher: The indiviual steps of the stairs can be of different height (including height 0); for instance, the working area might look like this:

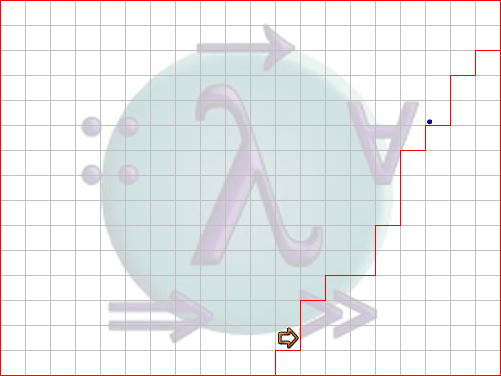
Can you think of a way to change our program so that the robot can still accomplish the same task? You can use our existing solution in file example4a.hs and try to modify it accordingly. Hint: Only the functions stair_up and stair_down have to be adapted...

When you have succeeded you can compare your solution to the one in example4b.hs (there are of course several solutions possible, so you don't necessarily need to have the same).

Now that you have basically seen everything, go on and try to solve some examples on your own in chapter 4.

by Lars Otten, 2004

http://lotten.net/